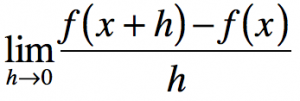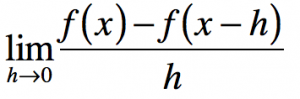Today we continued examining the connections between the graph of a function and the graph of its derivative.  We noticed that when the tangent is at the top of a hill or the bottom of a valley, the tangent line is horizontal….or has a zero slope.  We also noticed that when the original curve has tangents with negative slopes, the slope function occurs below the x-axis.  Further, when the tangents have positive slopes, the slope function is graphed above the x-axis.

We discussed  how every curve can be created by a small arc.  We can then rotate duplicates of this  arc and create almost every curve.  We briefly discussed how the curve increases and decreases as we move from left to write.  We identified pieces which can be described as….

• positive, increasing slopes
• positive, decreasing slopes
• negative, increasing slopes
• negative, decreasing slopes

You might check out the following applet derivative puzzles to practice identifying the graphs of derivatives without knowing the equation of the original function.

We continued discussing the connections of f and f’ graphs today.  We will continue to make observations such as a horizontal asymptote on the original function aligns with a root on the derivative function.  We also used our observations to determine the derivative of sin(x) and cos(x).

We continued our discussion of limit definitions of derivatives today.  We revisited the three definitions from yesterday and added the Alternative Definition of a derivative – .

We also investigated the connection the graph of a  function to the graph of its derivative.  We also explored the connections among the finite differences of a function, the degree of a function, and the number of possible derivatives.

We spent the majority of class today discussing how the Average Rate of Change (slope of a secant line) becomes the Instantaneous Rate of Change (slope of a tangent line).  We reviewed the Classic (limit) Definition of a Derivative:  .  We also talked about the Variation on the Classic Definition of .  We also practiced finding the derivative of a function using these definitions.  We closed the period while discussing the Symmetric Difference Quotient:  .

Today we discussed our first “short cut” to find instantaneous rates of change.  We reviewed the basic rule.  While we applied the rule to some routine problem which were already in the x^n format, we quickly moved to problems which had to be rewritten into the appropriate form.  We multiplied quantities out.  We simplified rational expressions.  We rewrote fractions from terms such as sqrt(x) to x^(1/2).

**Even though it may see backwards to learn the Power Rule before spending time fully developing the definitions of derivatives, we are learning the Power Rule first to allow us to check our answers when finding derivatives using our formal limit definitions. **

We also spent part of the period reviewing the ideas of AROC (average rate of change – slope of a secant line) and IROC (instantaneous rate of change – slope of the tangent line).  We will discuss three variations on these limit definitions over the next few days.